Delta Method implementation to estimate standard errors in a {tidyverse} workflow.
Installation
You can install the stable version from the CRAN with
install.packages("dplyr")Or the development version from GitHub with
remotes::install_github("JavierMtzRdz/tidydelta")
# Or
devtools::install_github("JavierMtzRdz/tidydelta") Theoretical Background
In general terms, the Delta Method provides a tool for approximating the behaviour of an estimator using Taylor Expansion, where is an estimator of a parameter , and is a function. To derive this result, we should begin with the observation that, according to the continuous mapping theorem, if implies assuming that is a continuous function (Vaart 2000, 25).
This observation allows us to take a step forward to decompose the theorem of the DM. Assuming that is not only continuous but also differentiable and further assuming that converges in distribution to a variable as the sample size increases, (Bouchard-Côté n.d., 87) we can employ Taylor Expansion to show that
Now, as the sample size becomes larger, the expression converges in distribution to (Vaart 2000, 25; Bouchard-Côté n.d.).
Given the previous result, we can rearrange the equations to show that
as grows larger. For this reason, it is not a surprise that one of the primary uses of the Delta Method is to approximate the variance of transformations of estimators.
The Multivariate Case
We often encounter scenarios where our can be expressed as a function of more than one parameter. For instance, we may be interested in the transformation of (Zepeda-Tello et al. 2022). In this case, we are dealing with a multivariate parameter space and the estimator becomes a random vector. Consequently, the asymptotic behaviour of the estimator can be seen as follows (Weisberg 2005, 79–80)
To approximate this scenario using the Delta Method, we need to compute the vector of all partial derivatives of with respect to each parameter . This vector is denoted as . With this vector, we can extend the Delta Method to the multivariate case stating that asymptotically
In this equation, represents the transpose of the gradient vector , and is the covariance matrix of the random vector (Weisberg 2005, 79–80).From this, we obtain that , which constitutes the function that is being implemented in this project.
Examples
Using tidydelta(), the following commands are equivalent:
# Load packages
library(tidydelta)
library(tidyverse)
# Simulate samples
set.seed(547)
x <- rnorm(10000, mean = 5, sd = 2)
y <- rnorm(10000, mean = 15, sd = 3)
bd <- tibble(x, y)
# Equivalent uses of tidydelta()
tidydelta(~ y / x,
conf_lev = .95
)
#> # A tibble: 1 × 6
#> y x T_n se lower_ci upper_ci
#> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 15.0 5.02 2.99 1.33 0.378 5.61
tidydelta(~ bd$y / bd$x,
conf_lev = .95
)
#> # A tibble: 1 × 6
#> y x T_n se lower_ci upper_ci
#> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 15.0 5.02 2.99 1.33 0.378 5.61
bd %>%
summarise(tidydelta(~ y / x,
conf_lev = .95
))
#> # A tibble: 1 × 6
#> y x T_n se lower_ci upper_ci
#> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
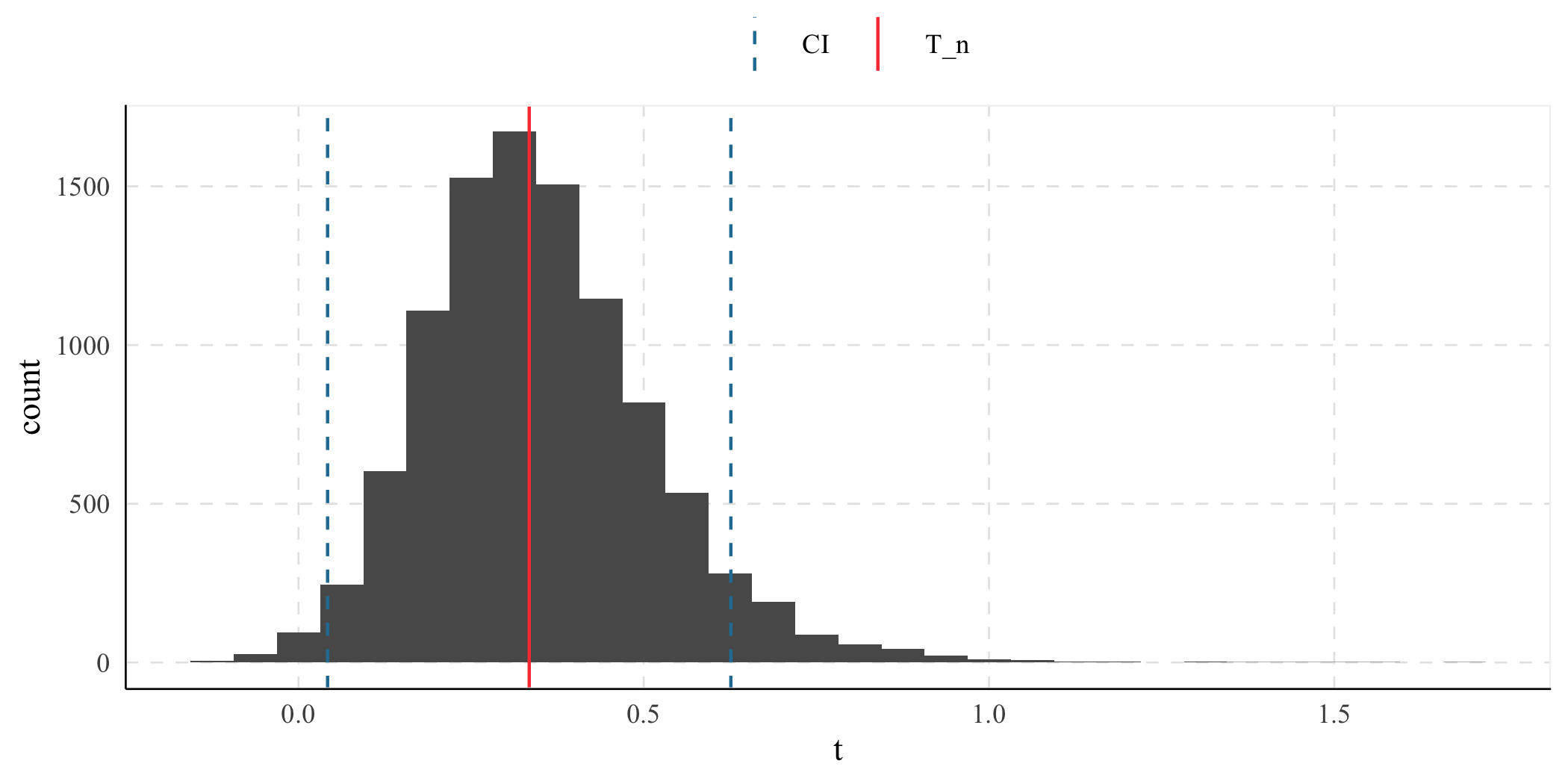
#> 1 15.0 5.02 2.99 1.33 0.378 5.61Now, the data frame is divided into samples to compare the transformation of the sample with the estimation of tidydelta(). In the real world, you would not need to compute the Delta Method if you have many samples, but it shows how it can be incorporated in a workflow with tidyverse.
(result <- bd %>%
summarise(tidydelta(~ x / y,
conf_lev = .95
)))
#> # A tibble: 1 × 6
#> x y T_n se lower_ci upper_ci
#> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 5.02 15.0 0.334 0.149 0.0422 0.626
ggplot() +
geom_histogram(
data = bd %>%
mutate(t = x / y),
aes(x = t)
) +
geom_vline(aes(
xintercept = result$T_n,
color = "T_n"
)) +
geom_vline(
aes(
xintercept = c(
result$lower_ci,
result$upper_ci
),
color = "CI"
),
linetype = "dashed"
) +
labs(color = element_blank())